小生境(Niche):来自于生物学的一个概念,是指特定环境下的一种生存环境,生物在其进化过程中,一般总是与自己相同的物种生活在一起,共同繁衍后代。例如,热带鱼不能在较冷的地带生存,而北极熊也不能在热带生存。把这种思想提炼出来,运用到优化上来的关键操作是:当两个个体的海明距离小于预先指定的某个值(称之为小生境距离)时,惩罚其中适应值较小的个体。
海明距离(Hamming Distance):在信息编码中,两个合法代码对应位上编码不同的位数称为码距,又称海明距离。例如,10101和00110从第一位开始依次有第一位、第四、第五位不同,则海明距离为3。
如果觉得有帮助,用Google学术搜索应该能找到这篇,在www.sciencedirect.com上也可以找到。读书笔记如下:
===========================================华丽丽的分割线=========================================
1. Introduction
两种比较普遍的处理多目标GA的方法:
- 把所有目标合并成一个目标函数,或者给某个集合只分配一个目标函数,以加权法为例,缺点是很难精确地确定权重,权重分配上一点点的不同可能导致相差很大的解;
- 确定Pareto解集或其有代表性的子集。
2. Multi-objective optimization formulation
有些问题的Pareto解集很大(可能无界),有效的方法是去找能代表Pareto解集的一系列解(the best-known Pareto set),尽可能满足3个要求:
- 尽可能接近真正的Pareto解集,并且理想地应当是Pareto解集的子集;
- 均匀分布;
- 能捕捉到Pareto解集的边界,也就是能到达目标函数的极端。
3. Genetic algorithms
交叉:让种群收敛到比较好的表现型;变异:向种群中注入基因的多样性,防止搜索过程太快地收敛到局部最优。
4. Multi-objective GA
通常,不同的多目标GA的差异体现在三个方面:适应度分配过程、精英主义(elitism)和多样化方法。
5. Design issues and components of multi-objective GA
5.1 Fitness functions
5.1.1 Weighted sum approaches
MBGA:每个个体在计算目标函数值时,各目标函数的权重 w={ w1, w2, ... , wk } 都不同;
RWGA:w={ w1, w2,…, wk } 是随机的。
优点——容易实现;缺点:如果Pareto解集是非凸的,不是所有的Pareto解都能被搜到。
5.1.2 Altering objective functions
VEGA:并列选择法。
优点——容易实现,与单目标GA的效率差不多;缺点:种群容易很快地收敛在某一目标上特别好但在其他目标上比较差的解。
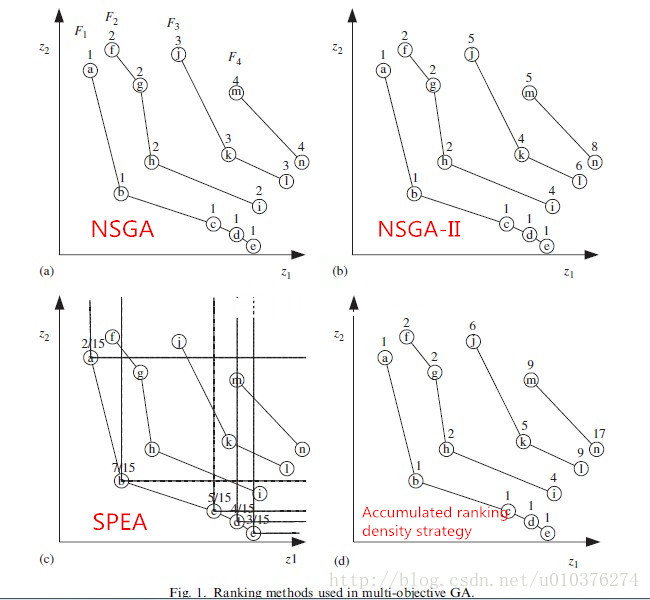
5.1.3 Pareto-ranking approaches
某一代中,依据目标函数值的排名(而不是目标函数值本身)给每个个体分配一个适应度。
NSGA-II:在目标函数空间里,惩罚那些被高密度Pareto解集支配的个体,如:(b)个体i;
SPEA:在目标函数空间里,给那些在不具有代表性区域内的个体分配更好的适应度,如:(c)个体a,有助于得到更加广泛、更加全局分布的Pareto解集;
Accumulated ranking density strategy :惩罚种群的冗余,即高密度区域的个体,如:(d)个体i、l、n。
5.2. Diversity: fitness assignment, fitness sharing, and niching
5.2.1 Fitness sharing
在归一化的目标空间,计算某一代个体之间的欧几里得距离(Euclidean distance) -> 根据欧几里得距离,计算小生境数(niche count) -> 每个个体的修正适应度=它的适应度/小生境数。
优点:目标空间里,密度高的区域内的个体会有较高的小生境数,适应度会因此变小,从而限制了在某个小生境内的快速繁殖;缺点:不好确定小生境的大小(niche size),计算的难度大。
MOGA(保持多样性的同时逼近真正的Pareto解集的算法),它计算适应度过程:用NSGA-II的方法计算每个个体的排名 -> 根据排名计算初始的适应度 -> 计算小生境数 ->每个个体的共享适应度(shared fitness value)=它的适应度/小生境数 -> 计算归一化的适应度。
SPEA2:一个个体的密度定义为离它最近的第k个个体与它的距离的倒数,个体的密度与它的小生境相似,并且确定参数k比确定小生境的大小更直接。
5.2.2 Crowding distance
NSGA-II:为某一代的个体排序并识别非支配解集 -> 计算每个个体针对每个目标函数的拥挤距离(crowding distance) ->计算个体所有目标函数的拥挤距离和,也就是该个体的拥挤距离。
优点:不通过适应度保持多样性,不需要自己确定参数(比如小生境的大小、k)。通常用作确定最后的选择个体。
5.2.3 Cell-based density
目标函数空间被分为K维房间(cell),每个房间里的个体数就是该房间里每个个体的密度,密度被用来保持多样性。
PESA:E是记录非支配解的仓库,某一代的个体都要根据是否被E中的个体支配,决定是否进入E,从而不断更新E,然后从E中选出密度小的个体做交叉变异。
PESA-II:选择的是房间,而不是个体。
RDGA:把目标函数空间分为许多K维房间 -> 更新每个目标函数的房间尺寸 -> 识别每个个体属于哪个房间,计算密度 -> 按照NSGA方法计算个体的排名 -> 把排名靠前和密度低的个体放到配对池中(两目标) -> 配对池中,被选择的父代只与所在房间/相邻房间中最好的个体交叉,且不允许被父代支配的个体进入房间,如果父代被自己的子代支配,就用子代代替父代。
优点:掌握了全局的密度分布,根据全局的密度搜索会向着密度小的区域进行;比小生境和计算周围密度的方法效率更高。
5.3 Elitism
精英主义(Elitism)的思想就是最好的个体应当保存到下一代,多目标GA有两种方法确保精英主义:
- 在群体里保存精英个体;
- 另外存储精英个体,并且把它们重新引入到群体中。
5.3.1 Strategies to maintain elitist solutions in the population
某一代的非支配个体直接复制到下一代,对其余个体选择交叉变异繁殖子代,填充到下一代。
缺点:如果某一代的非支配个体和产生的子代数目和,超过了群体大小的限制,这种方法就不行了。下面这些方法中,群体大小是一个重要的参数。
解决方法一:群体中只包含非支配个体,如果群体中个体数目达到上限,就移除(上限-下限)个个体,为了保持多样性,移除方法是对比两个随机选择的个体的小生境数,将小生境数大的个体从群体中移除。
解决方法二(NSGA-II):对某一代的个体做交叉变异得到子代 -> 这一代和子代合并到一个集合中 -> 将集合中的个体分为k个等级的非支配解集 { F1, F2, …, Fk } ?-> 计算每个个体的拥挤距离(按照5.2.2的方法) -> 从F1开始复制到下一代中,直到Ft加入下一代时,下一代的个体数刚好达到或者超过限制,如果超过了限制,就从Ft中选择拥挤距离小的个体填充到下一代。
5.3.2 Elitism with external populations
用E另外存储精英个体时,有两个关键问题:
- E中保存哪些个体:E保存非支配个体,且是不断更新;
- E有多大:通过剪枝来控制E的大小NE。
SPEA:把E中的个体分配到一个簇(cluster)ci中,所有簇构成C={ c1, c2, …, cM} -> 计算各个簇之间的距离 -> 把两个距离最近的簇合并成一个簇,重复前述步骤直到簇的个数<=N -> 从每个簇中选择到该簇中其他个体距离最近的个体,构成新的E,移除E中的其他个体。
SPEA2:把某一代群体Pt和Et合并 -> 计算其中每个个体的适应度 -> 把合并的集合全部复制到E(t+1)中,有两种情况:如果| E(t+1)|>NE,从E(t+1)移除一部分个体;如果| E(t+1)|,从合并的集合中再复制最好的个体填充。
5.4 Constraint handling
现实生活中的问题通常有一些限制条件,单目标GA从四个方面处理限制条件:
- 丢弃不可行解;
- 用惩罚函数降低不可行解的适应度;
- 构造算子使得只繁殖可行解;
- 把不可行解转变为可行解。
上述第二种方法是最常用的,但不能直接运用到多目标GA中,因为在多目标GA中,适应度是根据一个个体的非支配排名,而不是他的目标函数值分配的。解决方法是从群体中选择两个个体x和y,有以下三种情况:
- 一个可行一个不可行:可行的胜出;
- x, y都不可行:从群体中的不可行解里随机选择一组构成集合C,计算x, y以及C中所有个体的不可行性,对比x, y和C中最好个体的不可行性,如果x, y一个优于一个劣于最好个体,优于的个体胜出,如果x, y都优于/劣于最好个体,小生境数小的胜出;
- x, y都可行:从群体中的可行解里随机选择一组构成集合C,如果x, y一个支配C一个至少被C中的一个个体支配,前者胜出,否则小生境数小的胜出。
缺点:计算复杂度和增加的变量(例如,C的大小和小生境的大小),但可以通过调整减少。
Constraint-domination:个体x限制支配个体y,当满足x可行y不可行/x, y均不可行但x违背的限制条件更少/x, y均可行且x支配y。
Constraint tournament method:按照Constraint-domination的规则,重新定义非支配解集{ F1, F2, …, Fk }为非限制支配解集,执行“选择”步骤时,对任意两个个体x, y,如果x所在Fi和y所在Fj满足i,则x胜出,如果x, y在同一解集中,根据小生境数或拥挤距离决定胜者。优点:变量少,容易融合到多目标GA中。
Dominance-based tournament selection:个体x限制支配个体y,当满足对每个限制条件x的违背少于或与y相等,且至少有一个限制条件,x的违背少于y。
5.5 Parallel and hybrid multi-objective GA
精英主义和多样性的保持机制能提高多目标GA的效果,但是通常都会提高计算复杂度和存储空间,并行和分布式的GA是一种解决方法。
在单目标GA中,本地搜索算法的复合是最近用到的一种方法,本地搜索算法是:从一个初始个体开始 -> 用简单的扰动法则产生一些相邻的解 -> 如果相邻的解中有个体优于初始个体,替代。
优点:如果初始个体附近的解空间是凸的,查找局部最优的效果很好。关键点:选择初始个体;有很多非支配个体时,识别相邻解中的最优解。
6. Multi-objective GA for reliability optimization
多目标GA的运用
7. Conclusions
这篇论文关注各种多目标GA的构成要素和实现时遇到的突出问题;
Pareto解集需要被削减为一个有代表性的小集合,要使计算保持在合理的层次必须控制它的大小;
实现时必须考虑计算的复杂度,根据问题定制一些东西,例如,边界、假设、具体的计算方法等。

