

读完本文,可以去力扣解决如下题目:
787. K站中转内最便宜的航班(Medium)
毕业季,对过去也许有些欢乐和感伤,对未来也许有些迷茫和向往,不过这些终究是过眼云烟,迟早会被时间淡化和遗忘。
在这段美好时光的末尾,确实应该来一场说走就走的毕业旅行,放肆一把,给青春画上一个完美的句号。
那么,本文就教给你一个动态规划算法,在毕业旅行中省钱,节约追求诗和远方的资本。

假设,你准备从学校所在的城市出发,游历多个城市,一路浪到公司入职,那么你应该如何安排旅游路线,才能最小化机票的开销?
我们来看看力扣第 787 题「K 站中转内最便宜的航班」,我描述一下题目:
现在有n个城市,分别用0,1…,n - 1这些序号表示,城市之间的航线用三元组[from, to, price]来表示,比如说三元组[0,1,100]就表示,从城市0到城市1之间的机票价格是 100 元。
题目会给你输入若干参数:
正整数n代表城市个数,数组flights装着若干三元组代表城市间的航线及价格,城市编号src代表你所在的城市,城市编号dst代表你要去的目标城市,整数K代表你最多经过的中转站个数。
函数签名如下:
int findCheapestPrice(int n, int[][]flights, int src, int dst, int K);
请你的算法计算,在K次中转之内,从src到dst所需的最小花费是多少钱,如果无法到达,则返回 -1。
比方说题目给的例子:
n=3, flights=[[0,1,100],[1,2,100],[0,2,500]], src=https://zhuanlan.zhihu.com/p/0, dst=2, K=0
航线就是如下这张图所示,有向边代表航线的方向,边上的数字代表航线的机票价格:
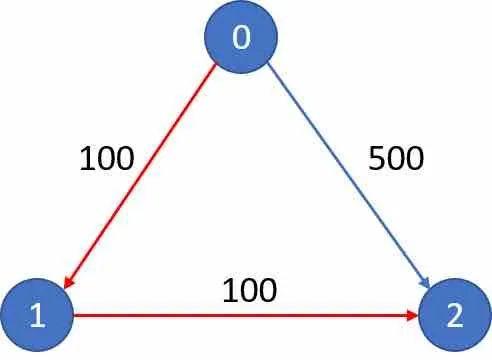
出发点是0,到达点是2,允许的最大中转次数K为 1,所以最小的开销就是图中红色的两条边,从0出发,经过中转城市1到达目标城市2,所以算法的返回值应该是 200。
注意这个中转次数的上限K是比较棘手的,如果上述题目将K改为 0,也就是不允许中转,那么我们的算法只能返回 500 了,也就是直接从0飞到2。
很明显,这题就是个加权有向图中求最短路径的问题。
说白了,就是给你一幅加权有向图,让你求src到dst权重最小的一条路径,同时要满足,这条路径最多不能超过K + 1条边(经过K个节点相当于经过K + 1条边。
我们来分析下求最短路径相关的算法。
我们前文 动态规划核心套路详解 中说过,求最值的问题,很多都可能使用动态规划来求解。
加权最短路径问题,再加个K的限制也无妨,不也是个求最值的问题嘛,动态规划统统拿下。
我们先不管K的限制,单就「加权最短路径」这个问题来看看,它怎么就是个动态规划问题了呢?
比方说,现在我想计算src到dst的最短路径:
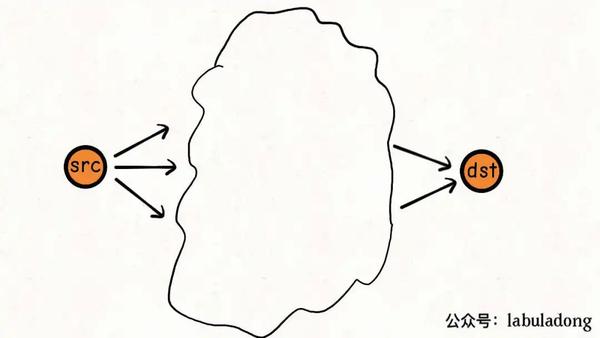
最小权重是多少?我不知道。
但我可以把问题进行分解:
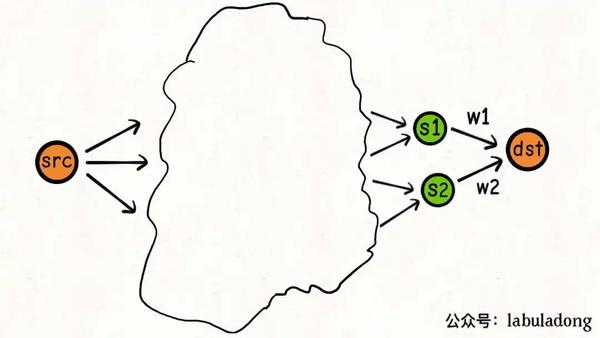
s1, s2是指向dst的相邻节点,它们之间的权重我是知道的,分别是w1, w2。
只要我知道了从src到s1, s2的最短路径,我不就知道src到dst的最短路径了吗!
minPath(src, dst)=min(
minPath(src, s1) + w1,
minPath(src, s2) + w2
)
这其实就是递归关系了,就是这么简单。
不过别忘了,题目对我们的最短路径还有个「路径上不能超过K + 1条边」的限制。
那么我们不妨定义这样一个dp函数:
int dp(int s, int k);
函数的定义如下:
从起点src出发,k步之内(一步就是一条边)到达节点s的最小路径权重为dp(s, k)。
那么,dp函数的 base case 就显而易见了:
// 定义:从 src 出发,k 步之内到达 s 的最小成本
int dp(int s, int k){
// 从 src 到 src,一步都不用走
if (s==src){
return 0;
}
// 如果步数用尽,就无解了
if (k==0){
return -1;
}
// ...
}
题目想求的最小机票开销就可以用dp(dst, K+1)来表示:
int findCheapestPrice(int n, int[][]flights, int src, int dst, int K){
// 将中转站个数转化成边的条数
K++;
//...
return dp(dst, K);
添加了一个K条边的限制,状态转移方程怎么写呢?其实和刚才是一样的:
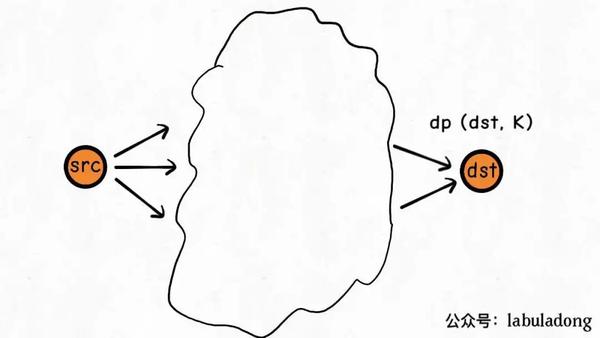
K步之内从src到dst的最小路径权重是多少?我不知道。
但我可以把问题分解:
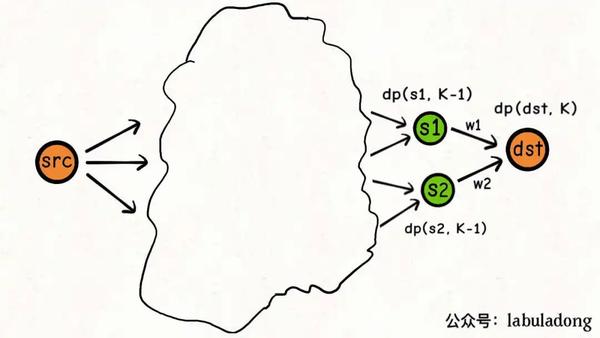
s1, s2是指向dst的相邻节点,我只要能够在K - 1步之内从src到达s1, s2,那我就可以在K步之内从src到达dst。
也就是如下关系式:
dp(dst, k)=min(
dp(s1, k - 1) + w1,
dp(s2, k - 1) + w2
)
这就是新的状态转移方程,如果你能看懂这个算式,就已经可以解决这道题了。
根据上述思路,我怎么知道s1, s2是指向dst的相邻节点,他们之间的权重是w1, w2?
我希望给一个节点,就能知道有谁指向这个节点,还知道它们之间的权重,对吧。
专业点说,得用一个数据结构记录每个节点的「入度」indegree:
// 哈希表记录每个点的入度
// to ->[from, price]
HashMap<Integer, List<int[]>> indegree;
int src, dst;
public int findCheapestPrice(int n, int[][]flights, int src, int dst, int K){
// 将中转站个数转化成边的条数
K++;
this.src=https://zhuanlan.zhihu.com/p/src;
this.dst=dst;
indegree=new HashMap<>();
for (int[]f : flights){
int from=f[0];
int to=f[1];
int price=f[2];
// 记录谁指向该节点,以及之间的权重
indegree.putIfAbsent(to, new LinkedList<>());
indegree.get(to).add(new int[]{from, price});
}
return dp(dst, K);
}
有了indegree存储入度,那么就可以具体实现dp函数了:
// 定义:从 src 出发,k 步之内到达 s 的最短路径权重
int dp(int s, int k){
// base case
if (s==src){
return 0;
}
if (k==0){
return -1;
}
// 初始化为最大值,方便等会儿取最小值
int res=Integer.MAX_VALUE;
if (indegree.containsKey(s)){
// 当 s 有入度节点时,分解为子问题
for (int[]v : indegree.get(s)){
int from=v[0];
int price=v[1];
// 从 src 到达相邻的入度节点所需的最短路径权重
int subProblem=dp(from, k - 1);
// 跳过无解的情况
if (subProblem !=-1){
res=Math.min(res, subProblem + price);
}
}
}
// 如果还是初始值,说明此节点不可达
return res==Integer.MAX_VALUE ? -1 : res;
}
有之前的铺垫,这段解法逻辑应该是很清晰的。当然,对于动态规划问题,肯定要消除重叠子问题。
为什么有重叠子问题?很简单,如果某个节点同时指向两个其他节点,那么这两个节点就有相同的一个入度节点,就会产生重复的递归计算。
怎么消除重叠子问题?找问题的「状态」。
状态是什么?在问题分解(状态转移)的过程中变化的,就是状态。
谁在变化?显然就是dp函数的参数s和k,每次递归调用,目标点s和步数约束k在变化。
所以,本题的状态有两个,应该算是二维动态规划,我们可以用一个memo二维数组或者哈希表作为备忘录,减少重复计算。
我们选用二维数组做备忘录吧,注意K是从 1 开始算的,所以备忘录初始大小要再加一:
int src, dst;
HashMap<Integer, List<int[]>> indegree;
// 备忘录
int[][]memo;
public int findCheapestPrice(int n, int[][]flights, int src, int dst, int K){
K++;
this.src=https://zhuanlan.zhihu.com/p/src;
this.dst=dst;
// 初始化备忘录,全部填一个特殊值
memo=new int[n][K + 1];
for (int[]row : memo){
Arrays.fill(row, -888);
}
// 其他不变
// ...
return dp(dst, K);
}
// 定义:从 src 出发,k 步之内到达 s 的最小成本
int dp(int s, int k){
// base case
if (s==src){
return 0;
}
if (k==0){
return -1;
}
// 查备忘录,防止冗余计算
if (memo[s][k]!=-888){
return memo[s][k];
}
// 状态转移不变
// ...
// 存入备忘录
memo[s][k]=res==Integer.MAX_VALUE ? -1 : res;
return memo[s][k];
}
备忘录初始值为啥初始为 -888?前文 动态规划核心套路,其实真没什么困难的。
查看更多优质算法文章 点击这里,手把手带你刷力扣,致力于把算法讲清楚!我的 算法教程 已经获得 90k star,欢迎点赞!